Probability and Random Processes

🙇‍♂️ | Links:

• Descriptive Statistics
  • Statistics
  • Inferential Statistics
  • Representative Values
  • Observational vs. Experimental Data
• Basic Probability
  • Probability Calculus
  • Probability Model
    • Events
    • Sample Space
  • Event Algebra
    • Or
    • And
  • Probability of Events
    • Non-Mutually Exclusive
    • Complement of an Event
    • Statistical Independence
  • Repeated Independant Trials
    • Sampling with Replacement
    • Sampling without Replacement
    • Order of Outcomes When Sampling Without Replacement
      • K-Tuples
    • The Rule of Product
    • Permutations of Unordered Outcomes
      • Permutations Without Replacement
    • Combinations of Non-Unique Outcomes
  • Conditional Probability
    • Bayes Theorem
    • Total Probability
• Random Variables
  • Discrete Probabilty Distributions
    • Probability Mass Function
    • Bernouli Random Variable
    • Binomial Random Variable
    • Geometric Random Variable
    • Poisson Random Variable
    • Uniform Random Variable
  • Continous RVs and Their Distributions
  • Common Continuous RVs
    • Exponential Random Value
    • Gaussian RV
    • Gaussian Q Values
  • Expectation
    • Moments
    • Central Moments
  • Entropy
• Multiple Random Variables
  • Discrete Random Variables
    • The Joint PMF
    • Independant Random Variables
  • Continuous Random Variables
    • Joint Distributions
    • Marginal PDFs
    • Correlation
    • Correlation Coefficient
    • Invariance of Expectation
  • Sum of Multiple RVs
    • PDF for \(X_1 + X_2\)
    • Notes on Sums of Independent RVs
    • Sums of Dependent RVs
  • Bivariate Gaussian
• Limit Theorems

Descriptive Statistics

Statistics

Statistics are the summarization of a set of data that has been collected, which demonstrates random variation. Extracting meaning from data.

Inferential Statistics

Inferential Statistics make inferences about a situation based on data, such as forecasting. Descriptive statistics can be the basis for inferences.

Representative Values

• Mean - The sum of all numbers in a list divided by the number of items in the list
• Median - The middle value in a list ordered from smallest to largest
• Mode - The most frequently occuring value in a list
• Range - [Min, Max]
• Variance - Average of deviation from the mean squared
• Standard Deviation - Measure of average absolute deviation
• Skewness - Measure of the shape of the distribution function
• Quantiles - Generalization of the median to percentiles

Observational vs. Experimental Data

Experimental Data involves manipulating objects to determine cause and effect in data. Observational Data refers to data extrapolated from naturally occurring events.

Basic Probability

Probability Calculus

Probability events have a total probability between zero and one.

\begin{equation} \text{Pr}[\textrm{An Event}] = 1 \end{equation}

An event that is sure to happen

The definition of probability for how often an event is observed can be related to the number of repetions of the experiment.

\begin{equation} \text{Pr}[\textrm{Heads}] = \frac{\textrm{Number } k \textrm{ of Heads in }N \textrm{ coin tosses}}{N \textrm{ coin tosses}} \end{equation}

Counting the probability of heads in a set of coin tosses

The larger the number of repetiions, the higher accuracy with which we can predict the likelihood of an event happening.

Probability Model

Events

Events are elements in the set of possible outcomes in an experiment.

Sample Space

The set of all possible outcomes for an experiment.

\begin{equation} S = {1,2,3,4,5,6} \end{equation}

The sample space for a dice roll

\begin{equation} A_1 = {1}, A_2 = {1,2,5} \end{equation}

Subsets containing events in the sample space

The complement of a subset \(A^C\) is the subset of all other events in the sample space which are not contained in \(A\).

Event Algebra

Or

The combination of two or more sets.

For \(A = \{1,2,5\}\) and \(B = \{3, 4\}\), \(A_1 + A_2 = \{1, 2, 3, 4, 5\}\)

And

The set of events which occur in two or more sets.

For \(A = \{1,2,3, 5\}\) and \(B = \{3, 4\}\), \(A_1A_2 = \{3\}\)

1. Mutual exclusion: \(AA^c = 0\)
2. Inclusion: \(AS = A\)
3. Double complement: \((A^C)^C = A\)
4. Commutation: \(A_1 + A_2 = A_2 + A_1\)
5. Associativity: \(A_1 + (A_2 + A_3) = (A_1 + A_2) + A_3\)
6. Distributivity: \(A_1 (A_2 + A_3) = A_1A_2 + A_1A_3\)
7. DeMorgan’s Law: \((A_1A_2)^c = (A_1)^C + (A_2)^C\)

Probability of Events

1. For any event \(A\): \(\text{Pr}[A] \geq 0\)
2. For the full set, \(\text{Pr}[S] = 1\)
3. If \(A\) and \(B\) are Mutually Exclusive then \(\text{Pr}[A + B] = \text{Pr}[A] + \text{Pr}[B]\)
4. Axiom 3 can be extended: \(\text{Pr}[A_1 + A_2 + ... ] = \text{Pr}[A_1] + \text{Pr}[A_2] + ...\)

Mutual Exclusivity refers to the fact that \(A\) and \(B\) will never occur simultaneously, ie \(AB = 0\).

Non-Mutually Exclusive

In cases where \(A\) and \(B\) can occur in the same set, Axiom 3 will not apply.

This is due to the fact that in overlapping events, the same area of probability will be counted twice, though it has no statistical importance.

\begin{equation} \text{Pr}[A_1 + A_2] = \text{Pr}[A_1] + \text{Pr}[A_2] - \text{Pr}[A_1A_2] \end{equation}

Non mutually exclusive OR

Complement of an Event

From expanding on these axioms, it can be seen that the complement of an event has a probability related to subtraction of itself from the sample space probability. If the chance of the event happening is known, the chance of an event not happening is found by subtracting this from absolute certainty.

\begin{equation} \text{Pr}[A^c] = 1 - \text{Pr}[A] \end{equation}

The complement of a set versus the whole

Statistical Independence

Two events \(A\) and \(B\) are said to be statiscally independent if:

\begin{equation} \text{Pr}[AB] = \text{Pr}[A]\text{Pr}[B] \end{equation}

Statistical independence

This refers to the fact that statistical data will happen independent of the preceding events. If you flip a coin, the probability of the next coin will be the same. If you take items from a bin, the probability of the next item being picked will go up, and is therefore dependent.

Repeated Independant Trials

From the rule of statistical independence, we can process repeated trials. \[\text{Pr}[H] = p\] \[\text{Pr}[T] = \text{Pr}[H^c] = 1 - p = q\] \[\text{Pr}[HHH] = ppp = p^3\] \[\text{Pr}[HTH] = pqp = p^2q\]

Coin Flips

Knowing that the probability of either event is 0.5, we can take the list of possible outcomes and calculate the probability. \[\begin{aligned} \text{Pr}[\textrm{At least two heads}] &= \text{Pr}[HHH] + \text{Pr}[HHT] + \text{Pr}[HTH] + \text{Pr}[THH] \cr &= ppp + ppq + pqp + qpp \cr &= (0.5)^3 + (0.5)^2*(0.5) + (0.5)^2*(0.5) + (0.5)*(0.5)^2 \cr &= 0.5 \end{aligned}\] \[\text{Pr}[\textrm{No heads}] = \text{Pr}[TTT] = q^3 = (0.5)^3 = 0.125\]

Sampling with Replacement

In this case, we consider an event where an event occurring does not subtract from a finite amount of events, ie a coin flip. In the case of heads or tails, there aren’t one less heads or tails. So it is as if we replace the event in our sample space.

Sampling without Replacement

Finite amounts of events that can be subtracted from the whole. If this event happens, it won’t happen again, as if we have taken our card from a deck of cards and not placed it back in the deck.

Order of Outcomes When Sampling Without Replacement

Cases when its important what order events occur in. Did we draw the Ace of Spades within the first 3 draws? The number of each event is not important.

K-Tuples

When a trial is repeated \(k\) times, we form a sample space of outcomes made up of \(k\) number of events.

The Rule of Product

How many possibilities are there for the formation of \(k\)-tuples, if there are \(N_i\) choices for the \(i\)th element?

\begin{equation} N_1 * N_2 * … N_k \end{equation}

The Rule of Product

By this rule, the number of possibilities when rolling a dice, then flipping a coin, will be \(6 * 2\). In the case where same number of outcomes are possible with each experiment, the number of \(k\)-tuples is \(N^k\), or \(2^k\) in the case of repeated coin tosses.

Permutations of Unordered Outcomes

We no longer care in what order outcomes occur, we are only concerned with the number of outcomes of a certain sort across all trials.

This involves the number of ways we can choose \(k\) objects in \(N\) choices.

Permutations Without Replacement

• Experiments with two or more possible outcomes
• These trials can be repeated independently for \(N\) times
• For each \(k\)th trial the outcome from the previous is removed
• Probabilities change for each consecutive trial

The resulting set is ordered, but as mentioned before, we only care about the number of possible permutations from these elements.

The number of possible sets is \(N!\) or \(N * (N-1) * (N-2) * ... 2 * 1\)

Example - The 13 cards of a suit in a deck of cards can be laid out in \(13!\) or \(6227020800\) different ordered sequences.

If you want just \(k\) draws from \(N\) possible ways to draw the object, the number of sets will instead be from \(N\) to \((N-k+1)\)

Consider this problem - Lisa has 13 different ornaments and wants to put 4 ornaments on her mantle. In how many ways is this possible?

Using the product rule, Lisa has 13 choices for which ornament to put in the first position, 12 for the second position, 11 for the third position, and 10 for the fourth position. So the total number of choices she has is \(13 * 12 * 11 * 10\). Using the factorial notation, the total number of choices is \(\frac{13!}{9!}\).

From this example, we can see that if we have \(N\) objects and want to arrange $k$ of them in a row, there are \(\frac{N!}{(N-k)!}\) ways to do this.

The notation for permutations is \(P^{13}_3\)

Combinations of Non-Unique Outcomes

A combination is a way of choosing elements from a set in which order does not matter.

Consider the following example: Lisa has 13 different ornaments and she wants to give 3 ornaments to her mom as a birthday gift (the order of the gifts does not matter). How many ways can she do this?

We can think of Lisa giving her mom a first ornament, a second ornament, a third ornament, etc. This can be done in \(P^{13}_3\) ways. However, Lisa’s mom is receiving all three ornaments at once, so the order Lisa decides on the ornaments does not matter.

There are \(3!\) reorderings of the chosen ornaments, implying the total number of ways for Lisa to give her mom an unordered set of 5 ornaments is \(\frac{13!}{3!10!}\).

\begin{equation} \frac{N!}{k!(N-k)!} \end{equation}

Rule of Combinations or Unordered Permutations

The notation for combinations is \(C^{N}_k\) = \({N}\choose{k}\)

Conditional Probability

A conditional probability is a probability that a certain event will occur given some knowledge about the outcome or some other event. \(P[A \mid B]\) is a conditional probability, it is read as “Probability of A given B”.

\begin{equation} \text{Pr}[A|B] = \frac{\text{Pr}[AB]}{\text{Pr}[B]} \end{equation}

Rule of Conditional Probability

A simple example - A fair 12-sided die is rolled. What is the probability that the roll is a 3 given that the roll is odd?

This is \(\text{Pr}[3 \mid \text{Odd}]\) or \(\frac{\text{Pr}[3]\text{Pr}[\text{Odd}]}{\text{Pr}[\text{Odd}]}\)

Because \(B\) has already happened, the intersection of \(B\) and \(A\) can have the \(B\) probability removed, because it is statistically redundant.

\begin{equation} \text{Pr}[A|B] = \frac{\text{Pr}[AB]}{\text{Pr}[B]} = \frac{\text{Pr}[B]\text{Pr}[A]}{\text{Pr}[A]} = \text{Pr}[B] \end{equation}

Conditional Probability if statiscally independent

Bayes Theorem

When attempting to compute the conditional probability of two events, when only one event is known, the Bayes Theorem allows for a workaround.

Consider \(H\) to be Hypothesis, and \(E\) to be Evidence

\begin{equation} \text{Pr}[H|E] = \frac{\text{Pr}[E|H] \text{Pr}[H]}{\text{Pr}[E]} \end{equation}

Bayes Theorem

We can expand the equation in the numerator to demonstrate fully: \[\text{Pr}[E|H]\text{Pr}[H] = \frac{\text{Pr}[EH]}{\text{Pr}[H]}*\text{Pr}[H] = \text{Pr}[EH] = \text{Pr}[HE]\]

Therefore, \(\text{Pr}[H \mid E]\) or \(\frac{\text{Pr}[HE]}{\text{Pr}[E]}\) can be found from \(\text{Pr}[E \mid H]\) and vice versa.

Total Probability

If \(A_1, A_2\), and \(A_3\) form a partition of the sample space, for each \(A_i\)

\begin{equation} \text{Pr}[A_i|B] = \frac{\text{Pr}[B|A_i] \text{Pr}[A_i]}{\text{Pr}[B]}, i = 1,2,3 \end{equation}

Total Probability

Knowing this, \(\text{Pr}[B]\) can be found from \(\text{Pr}[B \mid A_1] + \text{Pr}[B \mid A_2] + \text{Pr}[B \mid A_3]\)

\begin{equation} \text{Pr}[A_i|B] = \frac{\text{Pr}[B|A_i] \text{Pr}[A_i]}{\text{Pr}[B|A_1] + \text{Pr}[B|A_2] + \text{Pr}[B|A_3]}, i = 1,2,3 \end{equation}

Bayes General Rule

\begin{equation} \text{Pr}[B] = \text{Pr}[B|A_1] + \text{Pr}[B|A_2] + \text{Pr}[B|A_3] \end{equation}

Total Probability, when \(A_1\), \(A_2\), \(A_3\) form a partition

Random Variables

Random variables deal with a function \(X\) which maps a number \(x\) from the sample space \(S\). The number can be placed on the real number line, and a probability assigned to it based on its random occurrence.

Discrete Probabilty Distributions

Discrete random variables involve events with a discrete set of values.

Probability Mass Function

The Probability Mass Function, or PMF \(f_k [k]\) is a plotting of the probability of all events associated with a random variable \(K\). The sum of all amplitudes of the graph, \(\sum f_k [k]\) will be 1.

For a given value \(k\), the probability of this value is \(f_k[k] = \text{Pr}[K = k]\).

Consider \(f_k[k]\) the ranking of weights of each possible outcome. If an outcome is more probable, it is heavier, and plotted above the others.

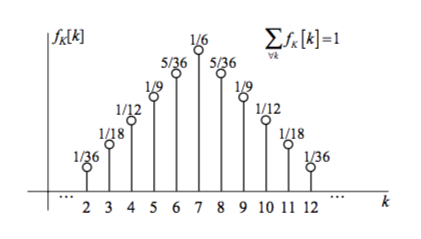
Probability Mass Function

Bernouli Random Variable

A Bernoulli RV is a discrete variable which will only produce values of \(1\) and \(0\). Therefore, the likelhood of one will be $p$ and the other will be \(1-p\).

Binomial Random Variable

The Bernoulli concept can be extended with combinatorics, for example in the base of binary transmission error. When detecting the error in the first \(k\)-bits of a \(n\)-bit transmission, \(f_K[k] =\) \(n\choose{k}\) \(p^k(1-p)^{(n-k)}\).

As shown in earlier sections, there are \(n\choose{k}\) possible variations of \(k\) bits in an \(n\)-bit long transmission. If our likelihood of non-error bits is \(p\), and error is \((1-p)\), the above will be intuitively correct.

Geometric Random Variable

Geometric RVs concern a wait for an event to happen. Should the expected event be given \(p\) probability, there will be \(k\) consecutive \((1-p)\) events before the \(p\) occurs. Therefore, as seen in the graph below, the event occuring at the second transmission will be \((1-p)^2p\).

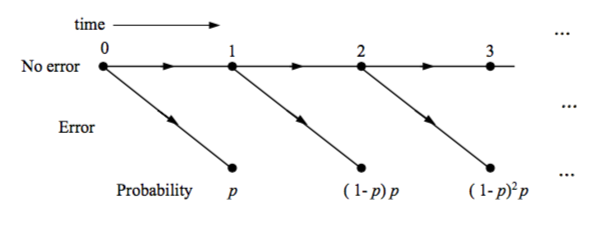
Geometric Random Variable

\begin{equation} f_K[k] = p(1-p)^k \end{equation}

Geometric Random Variable PMF (0 \(\leq\) k \(<\) \(\infty\))

Poisson Random Variable

For a situtation where revents occur randomly at a given rate \(\lambda\) over a certain time interval \(t\), the probability of \(k\) events happening within this time frame has been experimentally verified with \(\lambda t\) representing the average.

\begin{equation} f_K[k] = \frac{a^k}{k!}e^{-a} \end{equation}

Poisson Random Variable PMF

Note that for finding the probability of an event occurring after time \(t\), the probability becomes \(\text{Pr}[0] + \text{Pr}[1] + \text{Pr}[2] ... + \text{Pr}[t]\).

Uniform Random Variable

When all events are equally likely, the probability of each can be found easily from the uniform random variable PMF.

\begin{equation} f_K[k] = \frac{1}{n - m + 1} \end{equation}

Uniform Distribution

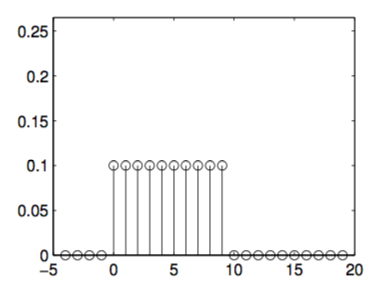
Continous RVs and Their Distributions

For values which can take on a continuum of values, such as voltage, velocity, and mass, new tools are used to analyze their probability. The probability of these events is determined using the Cumulative Distribution Function or CDF, which is written as \(F_X(x) = \text{Pr}[X \leq x]\).

By this notation we can see that by following the graph from left to right, the probability of the event occuring to the left of value \(x\) will be found by the amplitude of the CDF at that value. Therefore, as \(x \rightarrow \infty\), \(F_x \rightarrow 1\).

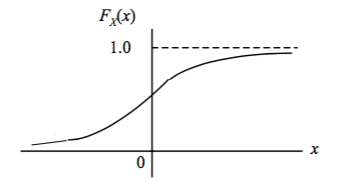
When finding the probability of a value occurring between points \(a\) and \(b\), their CDF values can be used. Remember this is Distribution, not Density, as we’ll see in the PDF below. By keeping this straight, their purposes should be easy to remember.

\begin{equation} \text{Pr}[a < X \leq b] = F_X(b) - F_x(a) \end{equation}

CDF Probability Within a Range (b \(>\) a)

The Probability Density Function or PDF is a derivative of the CDF that can also be used to find this probability:

\begin{equation} \text{Pr}[a < X \leq b] = \int_{b}^{a}f_X(x)dx \end{equation}

CDF Probability Within a Range (b \(>\) a) From Integration

This can be seen to be similar to the Probability Mass Function, as it will integrate over its full range to \(1 - \int_{\infty}^{\infty}f_X(x)dx = 1\). The difference is due to continous distributions being non-discrete - we can no longer say an item has mass, but points will now be denser (equivalent to heavier).

To use the PDF to find the probability of a number \(a + \Delta x\), we can multiply the PDF value at this point by the increment value to find the probability.

\begin{equation} \text{Pr}[a < X \leq a + \Delta x] = f_X(a) \cdot \Delta x \end{equation}

PDF Probability Within a Range (\(a < a + \Delta x\))

Integrating over a range (\(a, b\)) will also produce \(\text{Pr}[a < x \leq b]\) from the PDF.

Common Continuous RVs

Exponential Random Value

An extension of the Geometric Random Variable to the continuous realm, this represents a continuous graph of wait times where again \(\lambda\) represents the rate of arrival for an event as in Poisson RVs.

Its PDF follows \(f_X(x) = \lambda e^{-\lambda x}\)

Gaussian RV

The Gaussian or “normal” random variable arises naturally in numerous cases. It can be defined by its mean, \(\mu\), which will be the center of its bell shape, and its standard deviation \(\sigma\), which denotes the value in each direction it will pass before reaching \(60.7\%\) of its peak value.

\begin{equation} f_X(x) = \frac{1}{\sqrt{2\pi \sigma ^2}} e^{-(x-\mu)^2/2\sigma ^2} \end{equation}

The Gaussian PDF

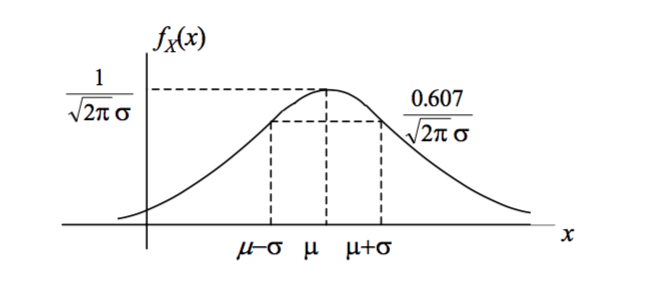
The square of the standard deviation, \(\sigma ^2\) is known as the variance, and is a measure of the total width of the bell between these points.

The standard form of the PDF, centered at \(0\) with a \(\sigma ^2\) \(=1\) can be used to express \(\text{Pr}[X \leq x]\):

\begin{equation} \Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{\infty}^{x}e^{-x^2/2} \end{equation}

The Standard Gaussian Function \[F_X(x) = \text{Pr}[X \leq x] = \Phi (\frac{x - \mu}{\sigma})\]

And as with any other CDF, \(\text{Pr}[a < x \leq b] = F_X(b) - F_x(a)\)

These \(\Phi\) values, which can be used as a CDF, as with other standard Gaussian values, can be found by table.

Gaussian Q Values

In cases where the probablity of values at either tail of a Gaussian is required, such as \(\text{Pr}[a < x \leq \infty]\), it is common to use \(Q\) functions.

\begin{equation} Q(x) = 1 - \Phi(x) \end{equation}

The Gaussian Q Function

When a value \(x\) is sought which is less than \(\mu\), the argument of the \(Q\) function will be negative, and define the left tail of the CDF. \(Q(-x) = 1 - Q(x)\).

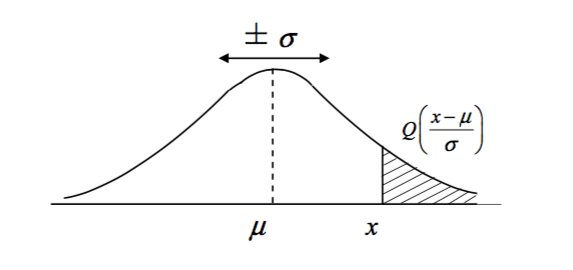
\begin{equation} \text{Pr}[X < x] = Q(\frac{x - \mu}{\sigma}) \end{equation}

The Gaussian Q Function

\begin{equation} \text{Pr}[X > x] = 1- Q(x) = Q(\frac{- x + \mu}{\sigma}) \end{equation}

The Gaussian Q Function with Negative Argument

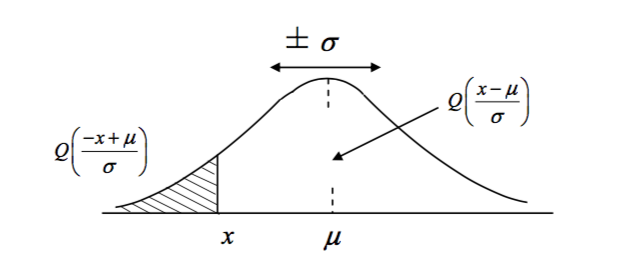\[\text{Pr}[a \leq x \leq b] = Q(\frac{b-\mu}{\sigma}) - Q(\frac{a-\mu}{\sigma})\]

Expectation

Expecation can be considered the average of the expected values in a sample space, where the values are weighted by their probability and summed.

\begin{equation} E{X} = \sum kf_K[k] \end{equation}

Expectation of a Discrete RV

For continuous random variables, when the PDF exists, the expectation can be calculated whenever the variable converges absolutely:

\begin{equation} E{X} = \int_{-\infty}^{\infty}xf_X(x)dx \end{equation}

Expectation of a Continuous RV

An important feature of the expectation is its invariance. \[E\{c\} = c\] \[E\{X + c\} = E\{X\} + c\] \[E\{cX\} = cE\{X\}\] \[E\{E\{X\}\} = E\{X\}\]

Moments

The moment is the produced when the \(X\) value of the expectation is raised to the \(n\) power. If \(g(X) = X^n\) for \(n\) = 1, 2, 3 \[E\{X^n\} = \int_{-\infty}^{\infty}x^nf_X(x)dx\]

Continous Moment \[E\{X^n\} = \sum k^n f_K[k]\]

Discrete Moment

The first moment is the mean, and each further \(n\) value is called the \(n\)th moment of the distribution.

Central Moments

The Central Moment is a mean of a random variable not centered at 0. Of particular importance is the variance, the square root of which will grant the width of the distribution. \[\sigma^2 = \text{Var}[X] = E\{(X-m_X)^2\}\]

The 2nd Central Moment \[m_X = E\{X\}\]

The mean of \(X\)

The Standard Deviation is represented as \(\sigma_X\), and is a measure of the width. \[\text{Var}[c] = 0\] \[\text{Var}[X + c] = \text{Var}[X]\] \[\text{Var}[cX] = c^2 \text{Var}[X]\]

Also note, \(\text{Var}[X] = E\{X^2\} - m_X^2\) - this method is much easier to solve than the initial method of finding variance.

Entropy

From the topic of information encoding, it was found that the definition of information for an event \(A\) is: \[I(A) = -\text{log}_2\text{Pr}[A] \text{bits}\]

And the average of information for two exclusive events \(A\) and \(B\): \[H = \text{Pr}[A]I(A) + \text{Pr}[B]I(B)\]

The definition of average information is in fact an expectation for two events that form a partition of a sample space.

For a partition \(A_i\) where \(I(A_i) = -\text{log}_2\text{Pr}[A_i]\), \[H = E\{I\} = \sum I(A_i)\text{Pr}[A_i] = \sum(-\text{log}\text{Pr}[A_i])\text{Pr}[A_i]\]

or, \[-\sum(\text{log}_2\text{Pr}[A_i])\text{Pr}[A_i]\]

Multiple Random Variables

Discrete Random Variables

The Joint PMF

Joint probability distribution can be thought of as \(\text{Pr}[(X \leq x \text{ and } Y \leq y)]\)

Or as \(F_{X,Y}(x,y)\) where \(F_X(x) = \text{Pr}[X \leq x]\) and \(F_Y(y) = \text{Pr}[Y \leq y]\)

A relationship can be deterministic, such as \(Y = 2X + 1\) or probabilistic, where probabilities of one value will affect the other.

Joint Probabilities refers to the probability of two variables taken together, such as \(\text{Pr}[(X \leq q) \text{ and } (Y \leq y)]\). To answer this, the Joint CDF, \(F_{X,Y}(x,y)\) must be found.

Recall from single random variable discussion, the PDF is the derivative of the CDF. Therefore, for cases where there are multiple variables: \[f_{X,Y}(x,y) = \frac{\partial}{\partial x} \frac{\partial}{\partial y}F_{X,Y}(x,y)\]

For continuous distributions, the variables \(x\) and \(y\) will be used, however discrete distributions use \(k\), \(l\), and so on.

From each joint distribution, individual distributions for each variable, or \textbf{Marginal Distributions} can be found. These are simply the PDFs of the individual random variables found in earlier sections.

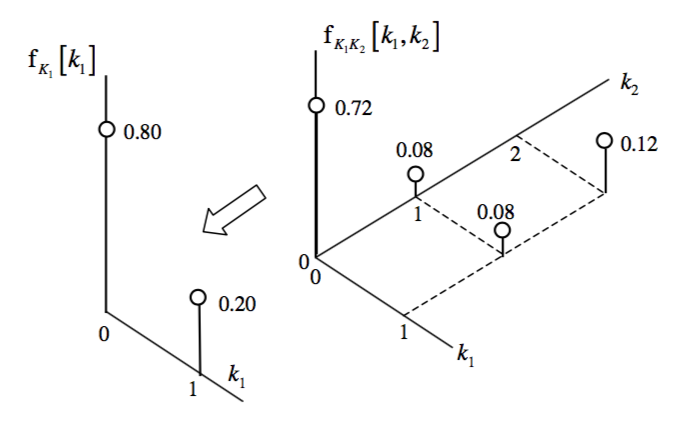
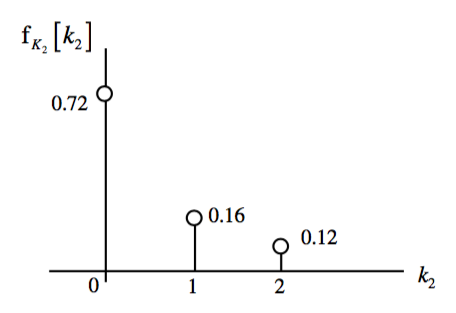\[f_{K_1}[k_1] = \sum\limits_{k2=-\infty}^\infty f_{K_1K_2}[k_1,k_2]\] \[f_{K_2}[k_2] = \sum\limits_{k1=-\infty}^\infty f_{K_1K_2}[k_1,k_2]\]

Independant Random Variables

From earlier in the course, events were defined as independent if \(\text{Pr}[AB]\) = \(\text{Pr}[A]\). Similarly, random variables can be said to be independent if the product of marginal distributions is equal to the joint distribution. \[f_{K_1K2}[k_1,k_2] = f_{K_1}[k_1]\cdot f_{K_2}[k_2]\] \[f_{X,Y}(x,y) = f_{X}(x)\cdot f_{Y}(y)\]

Notice that this is a special condition for random variables and does not apply in general! In particular, if two random variables are not independent, there is no way that the joint PMF can be inferred from the marginals. In that case the marginals are insufficient to describe any joint properties between \(K_1\) and \(K_2\).

Continuous Random Variables

Joint Distributions

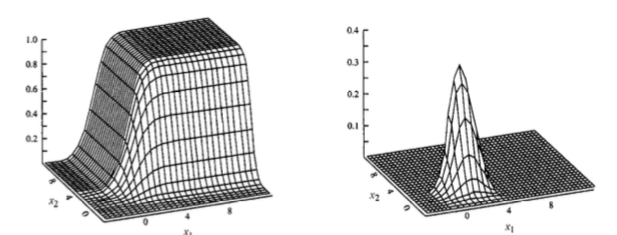
CDF: \(f_{X_1X_2}(x_1,x_2) = \frac{\partial^2F_{X_1X_2}(x_1,x_2) }{\partial x_1 \partial x_2}\)

PDF: \(F_{X_1X_2}(x_1,x_2) = \int_{-\infty}^{x_1} \int_{-\infty}^{x_2} f_{X_1X_2}(u_1,u_2)du_1du_2\)

Joint continuity can be proven if the PDF evaluates to 1.

Marginal PDFs

Similar to the marginal PMF, each distribution \(X_1\) and \(X_2\) can be described by its own PDF: \[f_{X_1}(x_1) = \int_{-\infty}^{\infty} f_{X_1X_2}(x_1,x_2)dx_2\] \[f_{X_2}(x_2) = \int_{-\infty}^{\infty} f_{X_1X_2}(x_1,x_2)dx_1\]

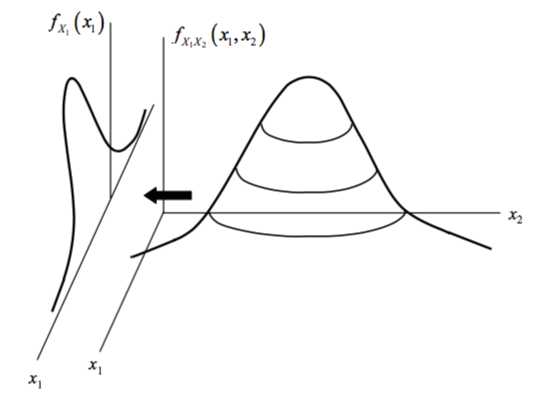
Correlation

Correlation is defined as the similarity between two random variables \(X_1\) and \(X_2\). Note that this is the multiplication of \(X_1\) and \(X_2\), not an “and”. \[r = E\{X_1X_2\}\]

The correlation is calculated using the expectation, worked out as the expectation for \(g\)(\(X_1,X_2\)) = \(X_1X_2\) based on the joint PDF for \(X_1\) and \(X_2\). \[r = E\{X_1X_2\} = \int \int x_1x_2f_{X_1,X_2}(x_1,x_2)dx_1dx_2\] \[r = E\{KL\} = \sum\limits_k \sum\limits_l klf_{K,L}(k,l)\]

The correlation can be misleading if both \(X_1\) and \(X_2\) have offsets built in to their means. The get around this, covariance is defined to remove their means. \[c = \text{Cov}[X_1,X_2] = E\{(X_1 - m_1)(X_2 - m_2)\}\]

Where \(m_1\) and \(m_2\) are the means of the two random variables taken seperately: \[m_1 = E\{X_1\} = \int x_1f_{X1}(x_1)dx_1\] \[m_2 = E\{X_2\} = \int x_1f_{X2}(x_2)dx_2\]

Note - Covariance is similar to variance, in that variance is a measure of how to the outcome of \(X_1\) can vary, while covariance is the measure of how the outcome of \(X_1\) and \(X_2\) can vary together.

Also similarly to variance: \[\text{Var}[X] = E\{X^2\} - m^2_x\] \[\text{Cov}[X_1,X_2] = E\{(X_1-m_1)(X_2-m_2)\} = E\{X_1X_2\} = m_1m_2 = r - m_1m_2\]

Correlation Coefficient

If comparing the correlation of one of pair of random variables to the correlation of another pair of random variables, both can be normalized based on their standar deviations: \[p = \frac{\text{Cov}[X_1,X_2]}{\sigma_1\sigma_2}\]

Where \(\sigma_1\) and \(\sigma_2\) are the standard deviations of \(X_1\) and \(X_2\).

Invariance of Expectation

If a random variable \(X\) with PDF \(f_X(x)\) is transformed to another random variable \(Y\) by a deterministic relationship, \(Y = g(X)\), e.g. \[Y = 3X +2\]

Then moments for \(Y\) can be obtained from the PDF of \(X\), without calculating the new PDF \(f_Y(y)\): \[E\{Y\} = \int g(x)f_X(x)dx\]

Sum of Multiple RVs

Because the expectation \(E\{\}\) is an integral, for the case that \(Y = X_1 + X_2\) for RVs \(X_1\) and \(X_2\): \[E\{Y\} = E\{X_1\} + E\{X_2\} = m_{X1} + m_{X2}\]

Therefore, because variance will distribute via multiplication: \[\text{Var}[Y] = E\{(Y-m_Y)^2\} = E\{(X_1 + X_2) - (m_{X_1} + m_{X_2}))^2\}\] \[= E\{((X_1 - m_{X_1}) + E\{(X_2 - m_{X_2}))^2\}\] \[= E\{(X_1 - m_{X_1})^2 + E\{(X_2 + m_{X_2})^2 + 2E\{(X_1 = m_{X_1})(X_2 - m_{X_2}\}\}\] \[\text{Var}[Y] = \text{Var}[X_1] + \text{Var}[X_2] + 2\text{Cov}[X_1,X_2]\]

\(\text{Var}[Y]\) therefore also depends on \(\text{Cov}[X_1,X_2]\). If \(X_1\) and \(X_2\) are independent, \(\text{Cov}[X_1,X_2] = 0\), and \(\text{Var}[Y] = \text{Var}[X_1] + \text{Var}[X_2]\).

PDF for \(X_1 + X_2\)

Begin by finding the CDF in a method similar to discrete RVs: \[\begin{aligned} F_Y(y) &= \text{Pr}[Y \leq y] = \text{Pr}[X_1 + X_2 \leq y] \cr &= \int (\int\limits^{y-x_1}_{-\infty}f_{X_1,X_2}(x_1,x_2)dx_2)dx_1 \end{aligned}\]

Note the limit of integration for the \(f_{X2}\) portion uses the upper limit as the equivalent of \(x_2\) (because \(y = x_1 + x_2\))

The PDF can be obtained from this because \(f_Y(y) = \frac{d}{dy}F_Y(y)\) \[f_Y(y) = \frac{d}{dy} ß\int (\int\limits^{y-x_1}_{-\infty}f_{X_1,X_2}(x_1,x_2)dx_2)dx_1\]

Because \(\frac{d}{dt}\int\limits_{-\infty}^{t-a}g(\theta)d\theta = g(t-a)\), \[f_Y(y) = \int\limits_{-\infty}^{\infty}f_{X_1,X_2}(x_1,y-x_1)dx_1\]

If the two RVs are independent, \[f_Y(y) = \int\limits^{\infty}_{-\infty}f_{X_1}(x_1)f_{X_2}(y-x_1)dx_1\]

Notes on Sums of Independent RVs

• When \(X_1\) and \(X_2\) are independent, \(\text{Cov}[X_1,X_2]\) = 0 and \(\text{Var}[Y]\) = \(\text{Var}[X_1]\) + \(\text{Var}[X_2]\), while \(m_Y = E\{Y\} = E\{X_1\} + E\{X_2\} = m_{X_1} + m_{X_2}\)
• If \(X_1\) and \(X_2\) have the same distribution, \(m_{X_1} = m_{X_2} = m\)

Sums of Dependent RVs

In the case of \(Y = X_1 + X_2\), if \(X_1\) and \(X_2\) are not independent, then: \[\begin{aligned} f_Y(y) &= \int\limits^{\infty}_{-\infty}f_{X_1,X_2}(x_1,y - x_1)dx_1 \cr m_Y &= E\{Y\} = E\{X_1\} + E\{X_2\} = m_{X_1} + m_{X_2} \cr\cr \text{Var}[Y] &= E\{(Y - m_Y)^2\} = \text{Var}[X_1] - \text{Var}[X_2] + 2\text{Cov}[X_1,X_2] \end{aligned}\]

Bivariate Gaussian

Two joint RVs with Gaussian characteristics together will have a joint Gaussian characteristic, called bivariate or multi-variate for more than 2.

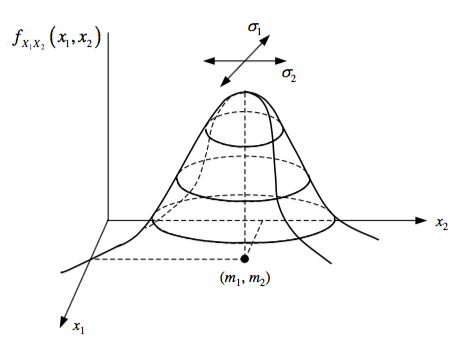
Limit Theorems

\[M_n = \frac{1}{n} \sum\limits^n_{i = 1}K_i\] \[E\{Y_n\} = mY_n = nm_x\] \[\text{Var}[Y_n] = \sigma_{Y_n}^2 = n\sigma^2_x\] \[Z_n = \frac{Y_n - mY_n}{\sigma Y_n} = \frac{Y_n - nm_x}{\sqrt{n}\sigma_x}\]

In other terms, when the number of trials approach large numbers, the mean of the trials will be \(N m_X\) and variance will be \(N \text{Var}[x]\), where \(x\) is a single trial. Then the new variable should have the characteristics of a Gaussian variable, with the mean and \(\sigma\) at these values.